Conventions

Coordinate systems

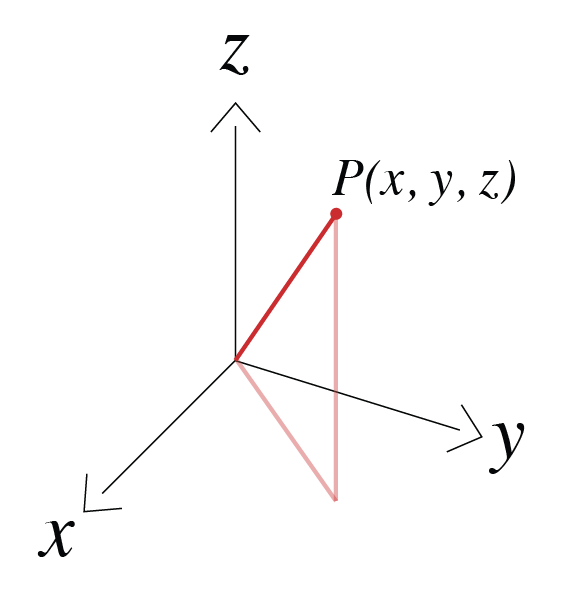
Cartesian

We use a right-handed coordinate system \((x, y, z)\) with z-positive up as shown in the Figure below.

Cylindrical

We again work with z-positive up and use \(\theta\) to denote the azimuthal angle, thus the coordinate system is defined as \((r, \theta, z)\).

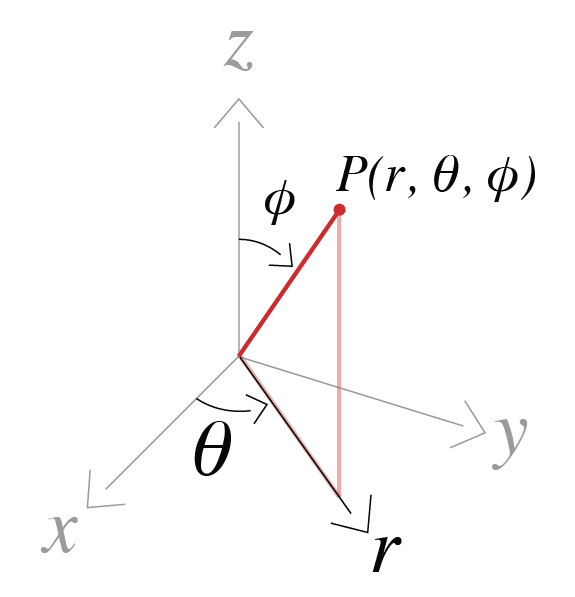
Spherical

We use \(r\) for the radial direction, \(\theta\) for the azimuthal direction, and \(\phi\) for the polar direction as shown in the figure below.

Fourier Transform

For analysis and solutions in the frequency domain we use the \(e^{i \omega t}\) Fourier transform convention. Thus, we define our Fourier Transform pair as

\[ \begin{align}\begin{aligned}\begin{split}F(\omega) = \int_{-\infty}^{\infty} f(t) e^{- i \omega t} dt \\\end{split}\\f(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega) e^{i \omega t} d \omega\end{aligned}\end{align} \]

where \(\omega\) is angular frequency, \(t\) is time, \(F(\omega)\) is the function defined in the frequency domain and \(f(t)\) is the function defined in the time domain.