geoana.em.static.MagneticDipoleWholeSpace.magnetic_flux_density

MagneticDipoleWholeSpace.magnetic_flux_density(xyz, coordinates='cartesian')

Compute magnetic flux density produced by the static magnetic dipole.

This method computes the magnetic flux density produced by the static magnetic dipole at gridded xyz locations provided. Where \(\mu\) is the magnetic permeability of the wholespace, \(\mathbf{m}\) is the dipole moment, \(\mathbf{r_0}\) the dipole location and \(\mathbf{r}\) is the location at which we want to evaluate the magnetic flux density \(\mathbf{B}\):

\[\mathbf{B}(\mathbf{r}) = \frac{\mu}{4\pi} \Bigg [ \frac{3 \Delta \mathbf{r} \big ( \mathbf{m} \cdot \, \Delta \mathbf{r} \big ) }{| \Delta \mathbf{r} |^5} - \frac{\mathbf{m}}{| \Delta \mathbf{r} |^3} \Bigg ]\]

where

\[\mathbf{\Delta r} = \mathbf{r} - \mathbf{r_0}\]

For reference, see equation Griffiths (1999).

Parameters:

xyz(…, 3) numpy.ndarray

gridded locations at which we calculate the magnetic flux density

coordinates: str {‘cartesian’, ‘cylindrical’}

coordinate system that the location (xyz) are provided. The solution is also returned in this coordinate system. Default: “cartesian”

Returns:

(…, 3) numpy.ndarray

The magnetic flux density at each observation location in the coordinate system specified in Teslas.

Examples

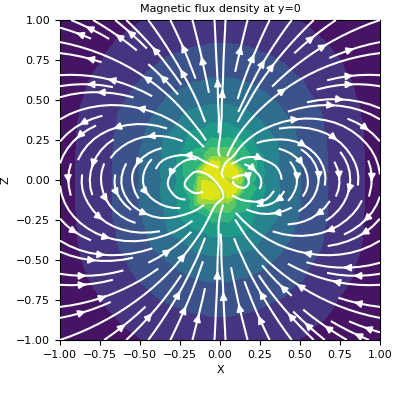
Here, we define a z-oriented magnetic dipole and plot the magnetic flux density on the xy-plane that intercepts y=0.

>>> from geoana.em.static import MagneticDipoleWholeSpace
>>> from geoana.utils import ndgrid
>>> from geoana.plotting_utils import plot2Ddata
>>> import numpy as np
>>> import matplotlib.pyplot as plt

Let us begin by defining the magnetic dipole.

>>> location = np.r_[0., 0., 0.]
>>> orientation = np.r_[0., 0., 1.]
>>> moment = 1.
>>> dipole_object = MagneticDipoleWholeSpace(
>>>     location=location, orientation=orientation, moment=moment
>>> )

Now we create a set of gridded locations and compute the vector potential.

>>> xyz = ndgrid(np.linspace(-1, 1, 20), np.array([0]), np.linspace(-1, 1, 20))
>>> B = dipole_object.magnetic_flux_density(xyz)

Finally, we plot the vector potential on the plane. Given the symmetry, there are only horizontal components.

>>> fig = plt.figure(figsize=(4, 4))
>>> ax = fig.add_axes([0.15, 0.15, 0.8, 0.8])
>>> plot2Ddata(xyz[:, 0::2], B[:, 0::2], ax=ax, vec=True, scale='log')
>>> ax.set_xlabel('X')
>>> ax.set_ylabel('Z')
>>> ax.set_title('Magnetic flux density at y=0')

(Source code, png, pdf)