geoana.em.static.PointCurrentWholeSpace.potential

PointCurrentWholeSpace.potential(xyz)

Electric potential for a point current in a wholespace.

This method computes the potential for the point current in a wholespace at the set of gridded xyz locations provided. Where \(\rho\) is the electric resistivity, I is the current and R is the distance between the location we want to evaluate at and the point current. The potential V is:

\[V = \frac{\rho I}{4 \pi R}\]

Parameters:

xyz(…, 3) numpy.ndarray

Locations to evaluate at in units m.

Returns:

V(…, ) np.ndarray

Electric potential of point current in units V.

Examples

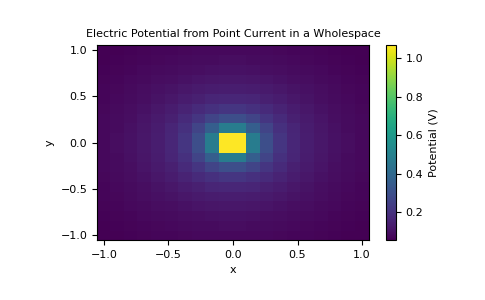
Here, we define a point current with current=1A and plot the electric potential as a function of distance.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from geoana.em.static import PointCurrentWholeSpace

Define the point current.

>>> rho = 1.0
>>> current = 1.0
>>> simulation = PointCurrentWholeSpace(
>>>     current=current, rho=rho, location=None,
>>> )

Now we create a set of gridded locations, take the distances and compute the electric potential.

>>> X, Y = np.meshgrid(np.linspace(-1, 1, 20), np.linspace(-1, 1, 20))
>>> Z = np.zeros_like(X)
>>> xyz = np.stack((X, Y, Z), axis=-1)
>>> v = simulation.potential(xyz)

Finally, we plot the electric potential as a function of distance.

>>> plt.pcolor(X, Y, v)
>>> cb1 = plt.colorbar()
>>> cb1.set_label(label= 'Potential (V)')
>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.title('Electric Potential from Point Current in a Wholespace')
>>> plt.show()

(Source code, png, pdf)