geoana.gravity.PointMass.gravitational_field

PointMass.gravitational_field(xyz)

Gravitational field due to a point mass. See Blakely, 1996 equation 3.3.

\[\mathbf{g} = \nabla U(P)\]

Parameters:

xyz(…, 3) numpy.ndarray

Observation locations in units m.

Returns:

(…, 3) numpy.ndarray

Gravitational field at observation locations xyz in units \(\frac{m}{s^2}\).

Examples

Here, we define a point mass with mass=1kg and plot the gravitational field lines in the xy-plane.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from geoana.gravity import PointMass

Define the point mass.

>>> location = np.r_[0., 0., 0.]
>>> mass = 1.0
>>> simulation = PointMass(
>>>     mass=mass, location=location
>>> )

Now we create a set of gridded locations and compute the gravitational field.

>>> X, Y = np.meshgrid(np.linspace(-1, 1, 20), np.linspace(-1, 1, 20))
>>> Z = np.zeros_like(X) + 0.25
>>> xyz = np.stack((X, Y, Z), axis=-1)
>>> g = simulation.gravitational_field(xyz)

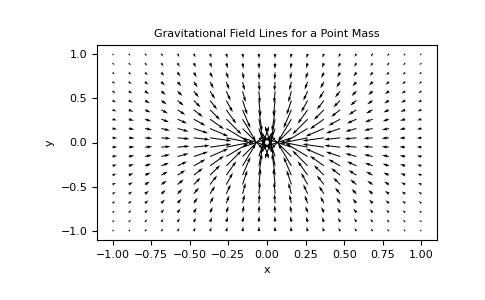
Finally, we plot the gravitational field lines.

>>> plt.quiver(X, Y, g[:,:,0], g[:,:,1])
>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.title('Gravitational Field Lines for a Point Mass')
>>> plt.show()

(Source code, png, pdf)